A continuación, os proponemos una actividad bastante divertida, manipulativa y, sobre todo, creativa para los niños, donde podrán desarrollar su imaginación a partir de sus conocimientos previos sobre la Geometría. Como siempre, incluiremos primero la parte legislativa y después la actividad propuesta.
Contenidos:
- La situación en el plano y en el espacio.
- Ángulos en distintas posiciones.
- Sistema de coordenadas cartesianas.
- Descripción de posiciones y movimientos.
- La representación elemental del espacio, escalas y gráficas sencillas.
- Formas planas y espaciales.
- Clasificación de triángulos atendiendo a sus lados.
- Concavidad y convexidad de figuras planas.
- Identificación y denominación de polígonos atendiendo a su número de lados.
- La circunferencia y el círculo. Sus elementos básicos: centro, radios, diámetro, cuerda, tangente.
- Cuerpos geométricos: elementos, relaciones y clasificación.
- Poliedros, tipos de poliedros, y sus elementos básicos: vértices, caras y aristas.
- Cuerpos redondos: cono, cilindro y esfera.
- Regularidades y simetrías.
Criterios de evaluación:
- Utilizar las nociones geométricas de paralelismo, perpendicularidad, simetría, geometría, perímetro y superficie. para describir y comprender situaciones de la vida cotidiana.
- Conocer las figuras planas: cuadrado, rectángulo, romboide, triángulo, trapecio y rombo.
- Comprender el método de calcular el área de un paralelogramo, triángulo, trapecio y rombo.
- Utilizar las propiedades de las figuras planas para resolver problemas.
- Conocer las características y aplicarlas para clasificar poliedros, prismas, pirámides, cuerpos redondos como conos, cilindros, esferas y sus elementos básicos.
- Interpretar representaciones espaciales realizadas a partir de sistemas de referencia y de objetos o situaciones familiares.
- Identificar, resolver problemas de la vida cotidiana, adecuados a su nivel, estableciendo conexiones entre la realidad y las matemáticas, y valorando la utilidad de los conocimientos matemáticos adecuados y reflexionando sobre el proceso aplicado para la resolución de problemas.
Estándares de aprendizaje:
- Identifica y representa posiciones relativas de rectas y circunferencias.
- Identifica y representa ángulos en diferentes posiciones: consecutivos, adyacentes, opuestos por el vértice...
- Clasifica triángulos atendiendo a sus lados y sus ángulos. Identificando las relaciones entre sus lados y sus ángulos.
- Calcula el área, el perímetro de: rectángulo, cuadrado y triángulo.
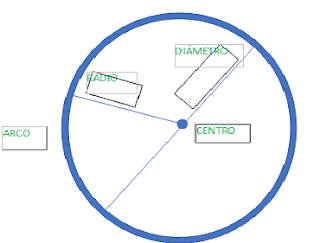
- Identifica y diferencia los elementos básicos de circunferencia y círculo: centro, radios, diámetro, cuerda, tangente y sector circular.
- Calcula perímetro y área de la circunferencia y del círculo.
- Utiliza la composición y la descomposición para formar figuras planas y cuerpos geométricos a partir de otras.
- Identifica y nombre polígonos atendiendo a sus números de lados.
Competencias clave:
- Matemática
- Lingüística
- Agilidad mental
- Aprender a aprender
Metodología:
Mediante esta actividad realizada con un vídeo, pretendemos que los alumnos desarrollen su capacidad visual y espacial, entre otras.
Queremos conseguir que sean capaces, tanto de recrear figuras a partir de una imagen, como de recrearlas por ellos mismo sin haber visto esa figura anteriormente.
En este caso, nuestra actividad está hecha a cámara rápida, de modo que a los alumnos se les enseñará la figura montada y ellos deberán recrearla, teniendo la posibilidad de que posteriormente revisen el proceso de cómo construirla con los pasos de nuestro vídeo.
Esto deberán hacerlos con todas las figuras propuestas.
ACTIVIDAD 1:
VIDEO
ACTIVIDAD 2:
FICHA DE GEOMETRÍA
1.-
¿Cuántos lados tiene un triángulo?
Si
todos los lados son iguales, ¿cómo se denomina?
Y
si un ángulo es con diferencia más grande que los otros dos, ¿cómo
se llama?
2.-
Contesta verdadero o falso justificando las respuestas:
-
El trapecio es el paralelogramo que sólo tiene dos lados opuesto paralelos.
-
Tres puntos no colineales se dice que determinan un plano.
-
Dos rectas contenidas en el plano que no tienen ningún punto en común se dice que son secantes.
-
Dos ángulos que tienen un lado común y cuyos interiores no se solapan se dice que son adyacentes.
- Una figura se dice que es cóncava, si y solo si, contiene el segmento PQ para cada par de puntos P y Q contenidos en la figura.
3.-
Señala las partes de la circunferencia.
RESPUESTAS:
1.-
¿Cuántos lados tiene un triángulo? 3
lados.
Si
todos los lados son iguales, ¿cómo se denomina? Triángulo
equilátero.
Y
si un ángulo es con diferencia más grande que los otros dos, ¿cómo
se llama?
Triángulo obtusángulo.
2.-
Contesta verdadero o falso justificando las respuestas:
-
El trapecio es el paralelogramo que sólo tiene dos lados opuesto paralelos. VERDADERO
-
Tres puntos no colineales se dice que determinan un plano. FALSO, determinan un ángulo.
- Dos rectas contenidas en el plano que no tienen ningún punto en común se dice que son secantes. FALSO, son paralelas.
- Dos ángulos que tienen un lado común y cuyos interiores no se solapan se dice que son adyacentes. VERDADERO.
-
Una figura se dice que es cóncava, si y sólo si, contiene el segmento PQ para cada par de puntos P y Q contenidos en la figura. FALSO, es convexa.
VIDEO SOBRE VAN HIELE
ACTIVIDAD 3:
Señala y
calcula, cuál es el perímetro de las siguientes figuras:
1)
2)
A) 13 B) 15 C)
10 D) 5
3)
RESPUESTAS:
1) P=18cm
2) P=13cm
3) P=7cm
PAPIROFLEXIA
Además de todo esto, también os mostramos unas ideas geniales para hacer animales mediante la papiroflexia. De este modo, a parte de que los niños desarrollarán al máximo su creatividad, serán participes de su propio desarrollo en la geometría, ya que estarán constantemente consiguiente formas geométricas.
Estos trabajos con papel son muy divertidos y variados, a la vez que divierten y ayudan a desarrollar las capacidades cerebrales de quienes lo realizan.
Un ejemplo para sacar provecho a este método, sería utilizarlo para la enseñanza de distintos polígonos, en este caso, los triángulos. Sus vértices y lados iguales o desiguales, nos ayudarán bastante a la hora de realizar dobleces, de modo que los niños irán comprendiendo su uso.
Sucesivamente, podremos repetir los procesos realizando formas animadas como animales, donde se formen rombos y cuadrados entre otros polígonos.
Así, se le darán indicaciones de los diferentes polígonos que deberán ir formando hasta llegar al resultado de una forma o figura final. (Para ello, previamente, deberemos haber explicado y repasado las diferentes formas geométricas que podeos encontrar, con sus diversas características).
Entre otros de sus objetivos podemos encontrar los siguientes: aumentar la coordinación y concentración, desarrollar la concentración visual y mental, aumentar la destreza y habilidad manual, ayudar en la comprensión de relaciones espaciales ( atrás, delante, arriba, abajo..), el reforzamiento de la atención y la memoria, contribuir al pensamiento lógico- matemático, y despertar la sensibilidad artística de los niños, ya que muchas veces lo pasamos por alto y no nos damos cuenta.
¡Aquí van las ideas más sencillas y divertidas que hemos encontrado, además de otras muchas que podéis encontrar en internet!.
ACTIVIDAD 5
Suma todos los triángulos de las dos estrellas y calcula cuántos hay en total.
RESPUESTA
- La estrella grande tiene 8 triángulos, y la estrella pequeña también. Si sumamos ambos triángulos tendremos un total de 16.
ACTIVIDAD 6: KAHOOT
https://play.kahoot.it/#/?quizId=e6c9b4ba-e3c6-4a25-9de7-85fd2187fc9e














No hay comentarios:
Publicar un comentario