CONCEPTOS DE TRIGONOMETRÍA

La Trigonometría es literalmente el estudio de las relaciones que existen entre todas las medidas (de lados y ángulos) de un triángulo. 

Originalmente la trigonometría se utilizaba para definir las relaciones entre los elementos básicos de un triángulo: los  seis elementos principales, es decir, los 3 lados y los 3 ángulos.
Esto es así debido a que no cualesquiera tres segmentos pueden servir y ejercer la función de los lados de un triángulo, estos deben cumplir una cierta relación para que el triángulo “cierre”.
Por otra parte, no cualquieras tres ángulos pueden ser los ángulos de un triángulo: los tres ángulos de un triángulo suman un ángulo llano, es decir 180º.

Su estudio es muy interesante y divertido siempre y cuando se aprenda paso a paso cada relación de la trigonometría. Pero en realidad, su mayor importancia resulta en que se trata de un recurso que facilita y posibilita la resolución de una gran cantidad de situaciones y problemas cotidianos.

Por ello, en muchas profesiones termina siendo una herramienta muy importante en todo lo relacionado con aplicaciones basadas en Geometría y distancias.

Podemos destacar geólogos, astrónomos, físicos, jardineros, carpinteros y otras profesiones entre otras en las que podemos hacer uso de la trigonometría.

 En cuanto al estudio de la trigonometría, esta se divide en dos enfoques muy diferentes:

1. El estudio de las figuras en el plano, esto es las que comúnmente llamamos  bidimensionales (dos dimensiones = plano). Esta es la rama llamada: trigonometría plana.
2. El estudio de las figuras que forman parte de la superficie de una esférica. Esta es la rama llamada: trigonometría esférica.

Nuestro enfoque en la trigonometría a modo de investigación, lo vamos a dividir en dos bloques: Trigonometría 1(medidas, ángulos), y Trigonometría 2(teoremas,senos, cosenos, resolución de triángulos).

Trigonometría 1:

En cuanto a sus conceptos básicos podemos encontrar los siguientes:

•  Punto: El punto no se define. Un punto geométrico es imaginado tan pequeño que
• carece de dimensión. Se suelen designar por letras mayúsculas (Punto A).
•  Línea: Conjunto de Puntos. o Línea Recta: Por dos puntos pasa una recta y solamente una. Dos rectas no pueden tener más que un solo punto común. Se suele designar por dos de sus puntos con el símbolo __ encima (AB). Una línea tiene una sola dimensión: longitud.
•  Cuerpos Geométricos: Tienen tres (3) dimensiones: largo, ancho y alto.  
• Superficies: Son los límites que separan a los cuerpos del espacio que los rodea. Tienen dos (2) dimensiones: largo y ancho. 

•  Plano: Es un conjunto parcial de infinitos puntos. Se representa por un paralelogramo y se nombra por tres de sus puntos no alineados o por una letra griega. (ABC o α). Si una recta tiene dos) puntos comunes con un plano, toda la recta está contenida en el plano. Por tres puntos no alineados pasa un plano y solamente uno.  

• Poligonales: también se llaman así a las líneas quebradas.  Sus segmentos reciben el nombre de lados y los puntos comunes de los lados se llaman vértices.                                  

• Ángulo: es la abertura formada por dos semirrectas (lados) con un mismo origen (llamado vértice).
• Bisectriz de un Ángulo: semirrecta que tiene como origen el vértice y divide al ángulo en dos ángulos iguales.

En cuanto a la clasificación de triángulos lo podemos clasificar de la siguiente manera.

 Por sus lados: 

1. Isósceles: tiene dos lados iguales (y dos ángulos) 
2. Equilátero: tiene sus tres lados iguales (los tres ángulos también son iguales). 
3. Escaleno: tiene sus tres lados diferentes. (los tres ángulos también son diferentes). 

Por sus ángulos (la suma de los tres ángulos = 180°): 

1. Acutángulo: tiene los tres ángulos agudos ( <90°) 
2. Obtusángulo: Tiene un ángulo obtuso (> 90°) 
3. Rectángulo: Tiene un ángulo recto (45°).  Los catetos son los lados que forman el ángulo recto, y la hipotenusa es el lado opuesto al ángulo recto.

Y su vez, en el triángulo, podemos encontrar las siguientes rectas:

Mediana: segmento trazado desde un vértice hasta el punto medio del lado opuesto. Un triángulo tiene tres (3) medianas, correspondiendo una por cada lado. (m)  El punto de intersección de las medianas se llama baricentro (G). 

Altura: perpendicular trazada desde un vértice, al lado opuesto o a su prolongación (h).  El punto de intersección de las alturas se llama ortocentro (O). 

Bisectriz: recta notable que corresponde a la bisectriz de un ángulo interior. El punto de intersección de las bisectrices se llama incentro (I). o

Mediatriz: perpendicular en el punto medio de cada lado. (M).  El punto de intersección de las mediatrices se llama circuncentro (K).

Trigonometría 2:

Tanto en la trigonometría como en la geometría debemos destacar el Teorema de Pitágoras, el cual afirma que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual  a la suma de los cuadrados de las longitudes de los catetos.(a2= b2 + c2).

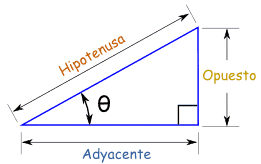
Este ámbito se centra en los triángulos rectángulos. Por ello, a la hora de resolver problemas matemáticos, nos servirá de gran ayuda, identificar primero sus diferentes lados, así como: hipotenusa, adyacente y opuesto).

                                           

En cuanto a las funciones más importantes de la trigonometría, destacamos: seno, coseno y tangente.
Cada una de ellas, es la longitud de un lado, dividida entre la longitud de otro, es decir:

Función seno:	sin(θ) = Opuesto / Hipotenusa
Función coseno:	cos(θ) = Adyacente / Hipotenusa
Función tangente:	tan(θ) = Opuesto / Adyacente

¡Os adjuntamos unos videos que os resolverán todas las dudas y explican todo más aún al detalle!.

SENO, COSENO, Y TANGENTE

TEOREMA DE TALES

TEOREMA DE PITÁGORAS